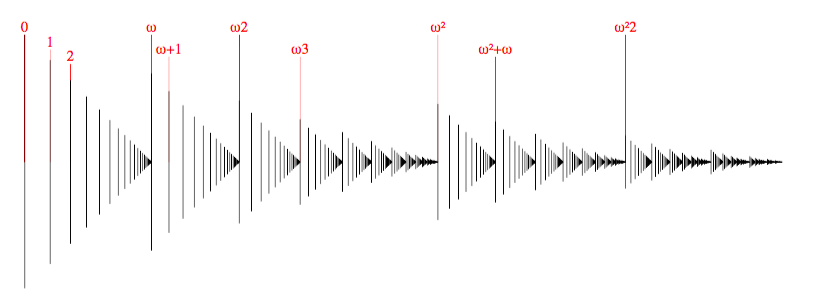
Hacia la década de 1880, Georg Cantor demostró que hay una infinidad de tamaños de infinitos. Existen dos tipos de números para cuantificar infinitos: cardinales y ordinales. Los primeros cuentan cuántos elementos tiene un conjunto mientras que los segundos representan la estructura de conjuntos bien ordenados—conjuntos ordenados linealmente donde cada subconjunto tiene un menor elemento:{},{0},{0,1},{0,1,2},…,ω={0,1,2,3,…},ω+1,…,2ω,3ω,…,ω2, ω3,…, ωω, y un etcétera muy muy grande que nunca termina pero que ha sido objeto de mucho estudio en la matemática.
Estas ideas están detrás de una serie de obras cuya duración será potencialmente infinita. Omega al cubo es un canon óctuple sobre conjuntos modelados en ω3 como estructuras encajadas entre sí a manera de membresías arregladas en jerarquías acumulativas a distintas escalas temporales con pasajes que rompen con ciclos anteriores para abrir nuevos inicios a partir de umbrales perceptuales.
He desarrollado versiones de omega elevada a potencias pequeñas y estoy trabajando en algoritmos que puedan ser indefinidamente recursivos para generar ‘omegas a la ene’ que puedan mapearse según umbrales perceptuales debido a que la resolución auditiva humana es mucho mayor que la visual. Esto implicará piezas en formato fijo, como en la pieza actual, pero también versiones en software para generar y visualizar estos conjuntos de manera interactiva.
Ficha técnica
| Autor: | Juan Sebastián Lach |
| Título: | Omega al cubo |
| Año: | 2017 |
| Género: | Composición |
| Técnica: | |
| Medidas: | |
| Duración: | |
| Referencia: | https://soundcloud.com/juan-sebastian-lach |
| Video/Audio: | |
| Créditos: |